The image is a record of the temporal and spatial changes in the objective world scene. Geometric transformations of images are the predominant factor of image changes. Naturally, although it makes significant sense to grasp the process of image geometric transformations, the numerical relationship of geometric transformations cannot be revealed directly from images themselves. If the changing process of this motion can be visualized from the abstract mathematical space, it will provide more possibilities to obtain better effectiveness of various visual tasks. Unfortunately, the relevant research of the visualization of the image geometric transformations is still in the blank stage, which becomes the obstacle to comprehend this motion group.

Facing this issue, a group of Chinese researchers at the Shenyang Institute of Automation (SIA) of Chinese Academy of Sciences have proposed a visualization model of image geometric transformations based on Riemannian manifold. The related study was published on the latest issue of IEEE ACCESS.

Researchers presented a new framework to visualize the changing process of geometric transformations in images based on Riemannian manifold. In particular, they defined a distance metric to compute the geodesic length on the SL(3,R) group on account of the fact that the lack of analytic expressions of Riemannian logarithmic map on the SL(3,R) manifold is the notorious obstacle for visualization. Once the hard-core issue of the distance metric is solved, the geometric transformations in images were further visualized based on the Riemannian stress majorization. The experimental results on diverse visual data demonstrated the effectiveness and performance of the proposed approach. 

This project first explores the possibility of proposing a Riemannian geometry-based framework to visualize the Sl(3,R) manifold, which establishes the bridge from the abstract geometric recognition space to the object recognition space. Not only is our framework valuable for analyzing motion groups of visual tasks, but also it will provide experience for other applications including medical imaging science and brain-computer interface. In the future, we will explore the possibility of creating deep representations of the manifold visualization with deep learning technology for better performance.

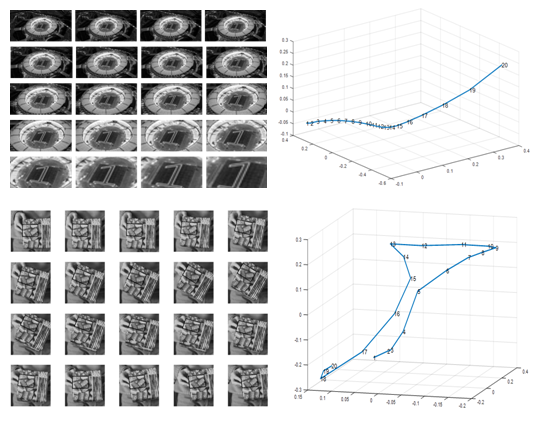
Visualization results of the geometric transformations