As one basic capability of autonomous vehicles, trajectory generation addresses the problem of determining feasible motions that drive a vehicle from initial states to target states given the associated vehicle models. This classic two–point boundary problem has been extensively studied recently. Nevertheless, it still remains unsolved considering the curvature and velocity constraints
imposed by the vehicle capability
To ensure the feasibility of the generated trajectories, researchers from Shenyang Institute of Automation (SIA), Chinese Academy of Sciences proposed quartic Bezier curve based trajectory generation algorithm considering both the curvature and velocity constraints. In the proposed algorithm, three basic constraints were considered to ensure feasibility of the trajectory: 1) The trajectory should satisfy the vehicle kinematic constraints; 2) The curvature should be continuous and bounded by the vehicle steering capability; The linear velocity to execute the generated trajectory should be continuous, acceleration–bounded and avoiding sideslip. It is rather complex to generate trajectories satisfying all these three constraints at the same time. Considering the vehicle kinematic model, the problem is firstly decoupled into two sub-problems: shape generation and velocity generation.
For shape generation, quartic Bezier curve is adopted to shape the trajectory. In order to fulfill the initial state (position, heading and curvature) and target state (position and heading) requirements, the curve is parameterized by 3 parameterized. Then, the curvature of the trajectory could be expressed as:
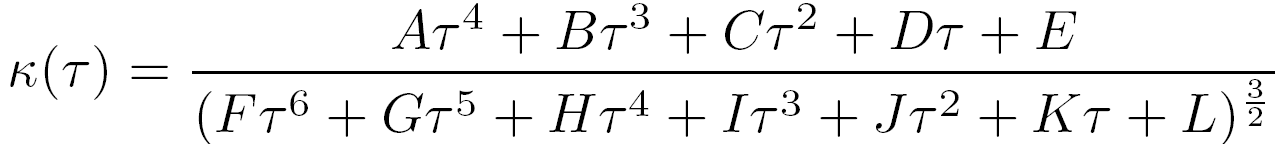
To further generate curvature-bounded trajectories, the problem is transformed to an optimization problem as:

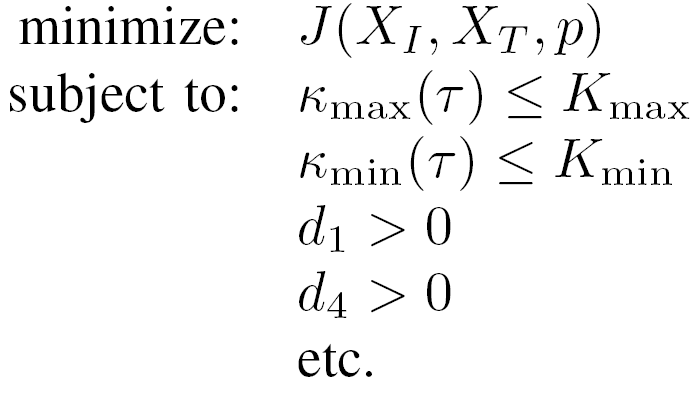
The overall shape generation problem is formulated as finding a set of parameters minimize the curvature change while satisfying the curvature boundary constraints. As shown in Fig. 1, simulation is conducted to verify the proposed algorithm.
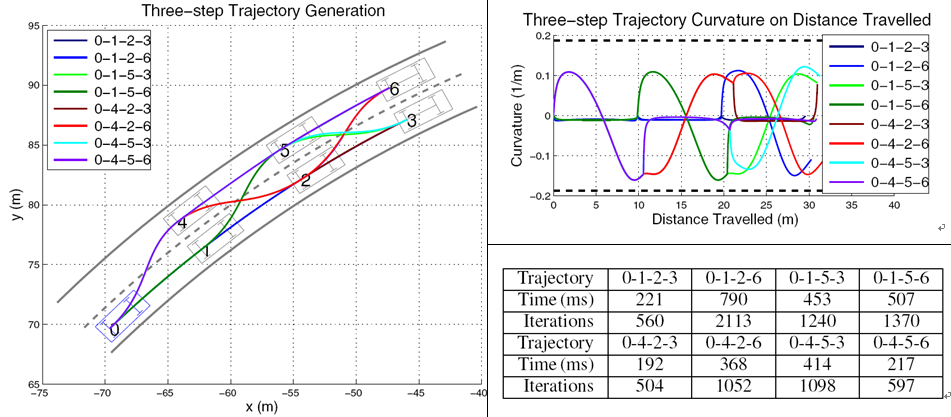
Fig.1 Left: Six states 1-6 are set for the vehicle to simulate lane keeping and lane changing maneuvers on the road. For example, the red line 0-4-2-6 illustrates the trajectory of maneuvers of two lane changes. Right Top: The curvature of the generated trajectories are bounded and continuous. Right Bottom: the time and iterations consumed to generate the trajectory. (Images provided by Chen Cheng, et. al)
For velocity generation, maximum velocity that could avoid side-slip at given curvature is first evaluated based on the simplified vehicle model:
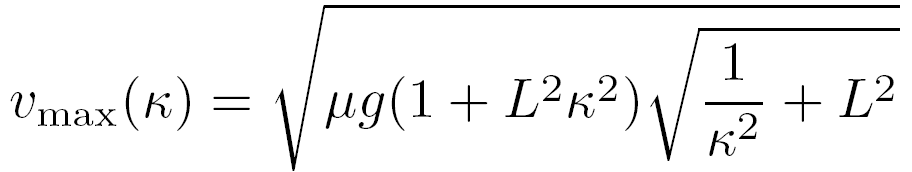
Considering the velocity limits, the initial and target velocities could be set first. Then, linear velocity profile could be obtained as:

where the trajectory length could be evaluated by integrating on the curve generated by shape generation. The acceleration should be bounded by vehicle acceleration capability. The time consumed to finish the trajectory is . As shown in Fig. 2, simulation is also conducted to verify the shape generation and velocity generation.
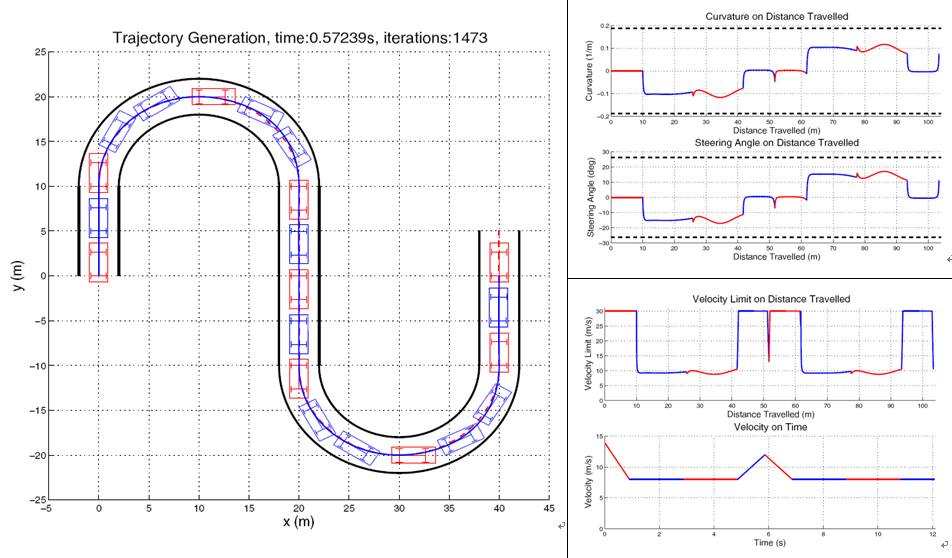
Fig. 2: Left: Seven target states are set for the vehicle to track the path. The trajectories are indicated by blue lines. Top Right: The curvature and steering changes with respect to distance travelled. The curvature and steering angle are bounded by the steering capability of the vehicle. Bottom Right: linear velocity limit and linear velocity with respect to distance travelled. (Images provided by Chen Cheng, et. al)
This work was published on the 2014 IEEE International Conference on Robotics & Automation (ICRA), May 31 - June 7, 2014 Hong Kong, China, 6108-6113.
It was partly supported by the State Key Program of National Natural Science of China (Grant No. 61035005).
CONTACT:
Ph.D Candidate Cheng Chen
Shenyang Institute of Automation, the Chinese Academy of Sciences
Email: chenc@sia.cn