|
|
| Automatic kinematic modeling of a modular reconfigurable robot |
| Author: |
|
Update times: |
2013-12-13 |
|
| Print | Close | Text Size: A A A |
|
|
Modular reconfigurable robots can achieve a high level of reliability for their flexibility to various tasks and environments. They have large configuration spaces, but it is too hard to manually enumerate all the configurations and their kinematics and dynamics in advance. Therefore, developing a method of automatically generating kinematics is an attractive and significant research topic. Researchers from Shenyang Institute of Automation (SIA), Chinese Academy of Sciences (CAS) proposed a method of generating the forward kinematics of a multi-chain modular reconfigurable robot. The robot mainly consists of joint modules, link modules, and end-effector modules. To deal with the multi-chain robots, the entries of the path matrix were employed to enable dyads to appear or not to appear in the kinematic equations. The researchers recognized a robot configuration by the communications between the host computer and modules via CAN bus and recognition lines, as shown in Fig. 1(a). Then, each assembly parameter ASM was obtained. Fig. 1(b) shows the recognition process. 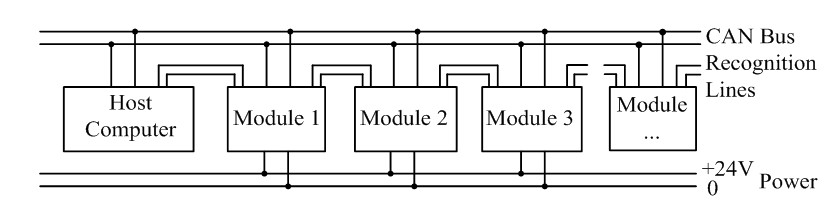
(a) Schematics of the communication system 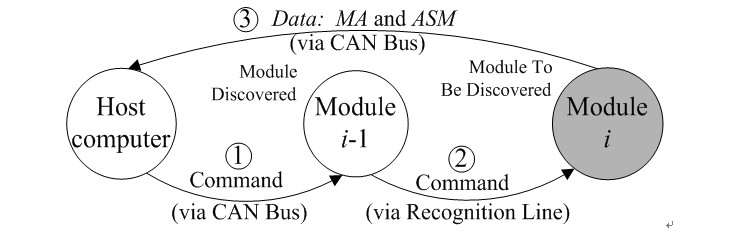
(b) Schematics of the discovery process of module i Figure 1. Schematics of the discovery process (Image provided by PAN Xin'an et.al) To analyze the recognized configuration, they employed four matrices: incidence matrix, degree matrix, asssembly incidence matrix(AIM), and path matrix. These matrices express a multi-chain configuration. The path matrix, which was obtained by a new simple algorithm, will benefit the kinematic modelling process for a multi-chain configuration robot. In order to describe the geometry and motion features of each module, they defined two frames attached to every connector of a module. The frames are input frame and output frame. Due to the path matrix does not incorporate any link information, a link is attached to its neighbor joint in kinematics, and the combination of the two modules are called a “dyad”, which is shown in Fig. 2. 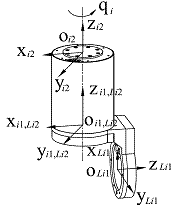
Figure 2. A dyad (Image provided by PAN Xin'an et.al) The initial pose of dyad i shown in Fig.2 can be derived as 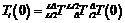
Considering that a configuration may have multiple chains, the entries of the path matirx was used to make a dyad active or inactive in a chain. Therefore, for a robot with n joints (end-effector included) and k chains, the initial pose of dyad i in chain j can be written as 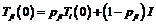
Subsequently, the initial poses of a multi-chain robot can be obtained as 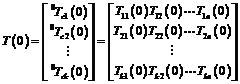
Next, the twists of the dyads should be obtained. Suppose that 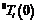 is given as is given as 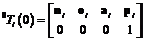
The twist of dyad i can be derived as 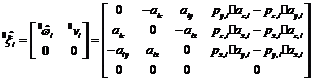
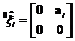 for prismatic joint, for prismatic joint,
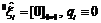
for end-effectors. 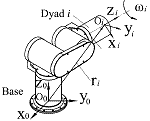 Figure 3. A twist with respect to the base frame Consequently, the researchers obtained the kinematics of a multi-chain robot as 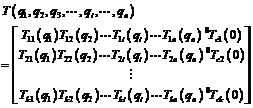
where  To verify the proposed method , a two chain robot was analyzed as an illustrative example. Furthermore, the comparison of the results between the proposed method and the D-H method also verifies the method. Finally, the researchers employed the proposed method with a reconfigurable robot MRRES to conducted an experiment. The MRRES and the experiment are shown in Fig. 4 and Fig. 5.  
Figure 4. Some MRRES modules (Image provided by PAN Xin'an et.al)     
Figure 5. Writing character experiment (Image provided by PAN Xin'an et.al) The proposed method is valid and reliable for a heterogeneous modular robot, and can be applied to both single-open-chain robots and multi-chain robots. Moreover, the method runs with little intervention by operators, and thus it achieves a high level of automation to some extent. This work was published on the Transactions of the Institute of Meassurement and Control, 35(7), 922-932. It was supported by the National High Technology Research and Development Program of China (863 Program) under Grant 2007AA041703, and the National Natural Science Foundation of China under Grant 60905048. CONTACT: PAN Xin’an Shenyang Institute of Automation, the Chinese Academy of Sciences Email:panxinan@sia.cn |
|
|
|